Welcome to the first of four posts that are designed to develop an understanding of the many-worlds interpretation of quantum mechanics. Quantum mechanics is a vast subject in itself, and while the Copenhagen interpretation is taught most frequently, I personally find the many-worlds interpretation to be easier to understand and a more logical approach.
But before we delve into the specifics of quantum mechanics, we should first look at the connections to classical mechanics, namely decoherence, wave-particle duality, and the uncertainty principle.
Many people will be familiar with the concept of wave-particle duality, most commonly exhibited in the diffraction pattern of a beam of electrons when fired through a double slit. However, it is also present in light waves, which come in quanta of energy, known as photons. Many experiments have been carried out in order to determine whether light and electrons are definitively either a wave or a particle, but depending on the conditions, both answers can be achieved. Just look at the diffraction pattern for an electron, and it seems to be a wave, but look at which slit it goes through, and it behaves as a particle.
A key term in quantum mechanics is operators. Operators are simply a function that relates to a classical observable. For example, the position function in the x direction is given simply by x, but the momentum in the x direction has a partial differential in the equation. The uncertainty principle states that when two operators don't commute (it matters in which order they are applied), then these two observables must always have a product uncertainty of ħ/2. So position and momentum in the x direction would be an example of this, as it matters when a differential is applied. The most difficult thing to understand about this is that this uncertainty is a distinct property, and not a result of inaccuracies during measurement.
 Most people who have heard the term quantum mechanics will have also heard of the Schrodinger equation. This equation is used to describe the physics of a quantum mechanical particle; it is essentially the quantum mechanical equivalent of Newton's Laws and conservation of energy. The Schrodinger equation comes in the form of a wave equation, and consists of a wavefunction, denoted by the Greek letter Phi, which precisely describes a particle, and a few operators. Operators describe a physical observable, everything has one, position, momentum, spin, energy, the list goes on and on. The Schrodinger equation employs two different energy operators. One side of the equation contains the Hamiltonian, denoted by H, which in turn consists of the Kinetic and Potential operators, which again consist of even more basic operators, moving down to just position. The other side contains an energy that depends only on time, denoted by E. A solution of the wavefunction that solves the equation is then found, and this describes the particle in varying degrees depending on the complexity of the Hamiltonian. The second equation here shows the expanded form of the time-independent Schrodinger equation. Time-independent simple means that we are assuming the energy to be constant over time.
Most people who have heard the term quantum mechanics will have also heard of the Schrodinger equation. This equation is used to describe the physics of a quantum mechanical particle; it is essentially the quantum mechanical equivalent of Newton's Laws and conservation of energy. The Schrodinger equation comes in the form of a wave equation, and consists of a wavefunction, denoted by the Greek letter Phi, which precisely describes a particle, and a few operators. Operators describe a physical observable, everything has one, position, momentum, spin, energy, the list goes on and on. The Schrodinger equation employs two different energy operators. One side of the equation contains the Hamiltonian, denoted by H, which in turn consists of the Kinetic and Potential operators, which again consist of even more basic operators, moving down to just position. The other side contains an energy that depends only on time, denoted by E. A solution of the wavefunction that solves the equation is then found, and this describes the particle in varying degrees depending on the complexity of the Hamiltonian. The second equation here shows the expanded form of the time-independent Schrodinger equation. Time-independent simple means that we are assuming the energy to be constant over time.
Quantum decoherence is a theory that brings together many of the phenomena found through quantum mechanics. Put simply, it is an effect where many quantum particles in a system coalesce into an object that follows classical laws. Expanding on this slightly, when quanta collide with each other, they form an entangled state, and this reduces the amount of interference that they can experience, and so these quanta start to obey the classical laws of physics. This is showing that in fact, there are no classical laws, just quantum laws adapted to a large scale. This also explains the diffraction pattern of the electron, while passing through the slit to produce the pattern, there is no decoherence, and so the electrons are free to interfere with each other. Yet when a detector is placed nearby, the huge system of quantum particles affects the electrons in such a way that forces them to no longer interact with each other, thus displaying particle like properties[1]. So instead of the environment affecting the system, it is actually the system affecting the environment, with the electrons joining the system and so being in an environment that allows no interference.
1. Joos E. Decoherence Website [Internet]. 2012 [cited 21 September 2016]. Available from: http://www.decoherence.de/

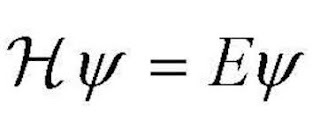
Schrodinger Equation, best Equation. Good start, will Quantum Tunnelling be a topic for another post? :)
ReplyDelete